Publications

2023

1. 

   Arbitrage-free neural-SDE market models

   Samuel N. Cohen, Christoph Reisinger, and Sheng Wang

   Applied Mathematical Finance, 2023

   Abs arXiv Bib HTML

   Modelling joint dynamics of liquid vanilla options is crucial for arbitrage-free pricing of illiquid derivatives and managing risks of option trade books. This paper develops a nonparametric model for the European options book respecting underlying financial constraints and while being practically implementable. We derive a state space for prices which are free from static (or model-independent) arbitrage and study the inference problem where a model is learnt from discrete time series data of stock and option prices. We use neural networks as function approximators for the drift and diffusion of the modelled SDE system, and impose constraints on the neural nets such that no-arbitrage conditions are preserved. In particular, we give methods to calibrate \textitneural SDE models which are guaranteed to satisfy a set of linear inequalities. We validate our approach with numerical experiments using data generated from a Heston stochastic local volatility model.

   @article{cohen2021mktmdl,
     title = {{Arbitrage-free neural-SDE market models}},
     author = {Cohen, Samuel N. and Reisinger, Christoph and Wang, Sheng},
     journal = {Applied Mathematical Finance},
     year = {2023},
     volume = {30},
     number = {1},
     pages = {1--46},
   }

2. 

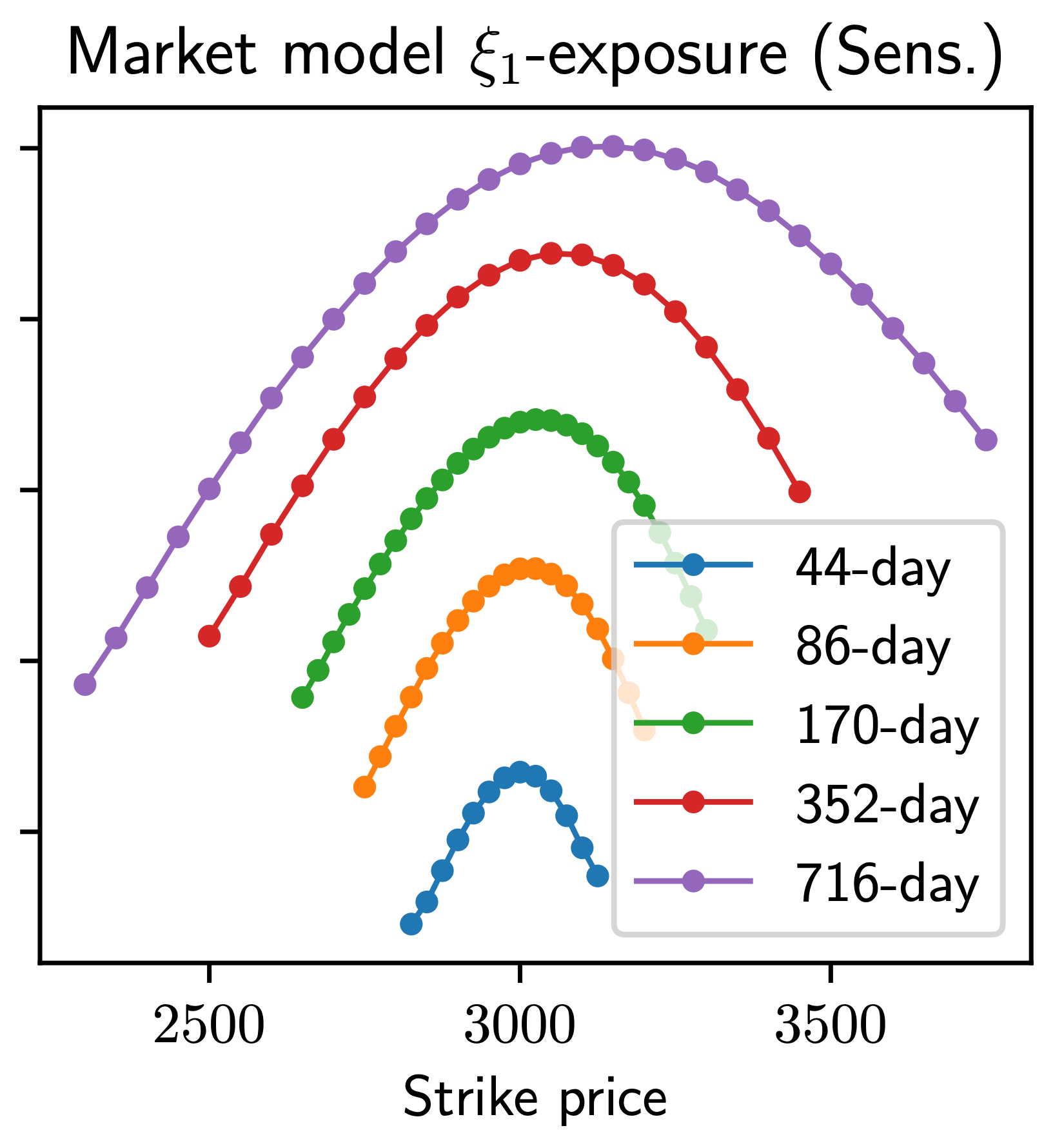   Hedging option books using neural-SDE market models

   Samuel N. Cohen, Christoph Reisinger, and Sheng Wang

   Applied Mathematical Finance, 2023

   Abs arXiv Bib HTML

   We study the capability of arbitrage-free neural-SDE market models to yield effective strategies for hedging options. In particular, we derive sensitivity-based and minimum-variance-based hedging strategies using these models and examine their performance when applied to various option portfolios using real-world data. Through backtesting analysis over typical and stressed market periods, we show that neural-SDE market models achieve lower hedging errors than Black–Scholes delta and delta-vega hedging consistently over time, and are less sensitive to the tenor choice of hedging instruments. In addition, hedging using market models leads to similar performance to hedging using Heston models, while the former tends to be more robust during stressed market periods.

   @article{cohen2022hedging,
     title = {Hedging option books using neural-SDE market models},
     author = {Cohen, Samuel N. and Reisinger, Christoph and Wang, Sheng},
     year = {2023},
     volume = {29},
     number = {5},
     pages = {366--401},
     journal = {Applied Mathematical Finance},
   }

2022

1. 

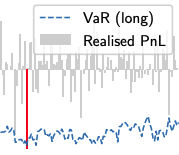   Estimating risks of European option books using neural stochastic differential equation market models

   Samuel N. Cohen, Christoph Reisinger, and Sheng Wang

   Journal of Computational Finance, 2022

   Abs arXiv Bib HTML

   In this paper, we examine the capacity of an arbitrage-free neural-SDE market model to produce realistic scenarios for the joint dynamics of multiple European options on a single underlying. We subsequently demonstrate its use as a risk simulation engine for option portfolios. Through backtesting analysis, we show that our models are more computationally efficient and accurate for evaluating the Value-at-Risk (VaR) of option portfolios, with better coverage performance and less procyclicality than standard filtered historical simulation approaches.

   @article{cohen2022estimating,
     title = {Estimating risks of European option books using neural stochastic differential equation market models},
     author = {Cohen, Samuel N. and Reisinger, Christoph and Wang, Sheng},
     journal = {Journal of Computational Finance},
     year = {2022},
     volume = {26},
     number = {3},
     pages = {33--72},
   }

2020

1. 

   Detecting and repairing arbitrage in traded option prices

   Samuel N. Cohen, Christoph Reisinger, and Sheng Wang

   Applied Mathematical Finance, 2020

   Abs arXiv Bib HTML

   Option price data are used as inputs for model calibration, risk-neutral density estimation and many other financial applications. The presence of arbitrage in option price data can lead to poor performance or even failure of these tasks, making pre-processing of the data to eliminate arbitrage necessary. Most attention in the relevant literature has been devoted to arbitrage-free smoothing and filtering (i.e., removing) of data. In contrast to smoothing, which typically changes nearly all data, or filtering, which truncates data, we propose to repair data by only necessary and minimal changes. We formulate the data repair as a linear programming (LP) problem, where the no-arbitrage relations are constraints, and the objective is to minimize prices’ changes within their bid and ask price bounds. Through empirical studies, we show that the proposed arbitrage repair method gives sparse perturbations on data, and is fast when applied to real-world large-scale problems due to the LP formulation. In addition, we show that removing arbitrage from prices data by our repair method can improve model calibration with enhanced robustness and reduced calibration error.

   @article{cohen2020detecting,
     author = {Cohen, Samuel N. and Reisinger, Christoph and Wang, Sheng},
     title = {Detecting and repairing arbitrage in traded option prices},
     journal = {Applied Mathematical Finance},
     year = {2020},
     volume = {27},
     number = {5},
     pages = {345--373},
   }